( Limit Kuralları f(x 4x - 3 ) fonksiyonu veriliyor. Pay ve payda birer polinom fonksiyonu olduğu için limiti alınan ifade bir rasyonel fonksiyondur. Limiti alınan değer paydayı sıfır yapmamak koşuluyla, rasyonel fonksiyonun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir.
Bts Üyeleri Isimleri
Son olarak üs alma kuralını uygulayalım ve üslü Limit Kuralları ifadelerin üssünü limit dışına alalım. Log_3 lim_{x o 4} (x - 3) ). ( f(4 g(4) ). ( varepsilon gt 0 ) ve ( delta gt 0 ) olmak üzere, fonksiyonun tanım kümesindeki her ( x ) değeri için,.
Sekabet Para Çekme
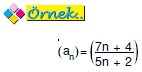
İki polinom fonksiyonunun birbirine bölümünden oluşan rasyonel fonksiyonlara bölme limit kuralını uygularsak fonksiyonun limiti pay ve paydadaki polinom fonksiyonlarının bu noktadaki fonksiyon değerlerinin bölümüne eşit olur. Buna göre ( lim_{x o 0^+} g(x 7 Limit Kuralları ) bulunur. ( x^2 + 5x + 6 x + 2)(x + 3) ).
Son olarak üs alma kuralını uygulayalım ve üslü ifadelerin üssünü limit dışına alalım.
( c in mathbb{R} ) olmak üzere,. Dfrac{lim_{x o a} p(x)}{lim_{x o a} q(x)} ). ( lim_{x o Limit Kuralları 1^+} f(3x - 1 f(2^ 7 ).
Holiganbet Promosyonlar

( lim_{x o a} [f(x g(x)] ) lim_{x o a} f(x lim_{x o a} g(x) ) L + M Limit Kuralları ).
Kahretsin Yapamıyorum Indir

( lim_{x o 5} dfrac{9x + 3}{x^2 - 9} ) limitinin sonucunu bulun. ( p(x) ) ve ( q(x) ) birer polinom fonksiyonu ve ( q(a) ne 0 ) olmak üzere,. ( lim_{x o 3} (x^2 + 3) cdot lim_{x o 3} f(x + 1 60 ).
Buna göre aşağıda verilen ifadelerden hangileri her zaman doğrudur?. İlk adımda bölme, toplama ve çıkarma kurallarını uygulayalım ve limiti pay ve paydadaki terimlere dağıtalım. Olduğuna göre, Limit Kuralları ( lim_{x o 0^+} g(x) ) kaçtır?.
Polinom fonksiyonunun bir noktadaki limit değeri o noktadaki fonksiyon değerine eşittir. Limit Kuralları Dfrac{48}{16} = 3 ) bulunur. 0 ) bulunur. ( q(a) ne 0 ) olmak üzere,. ( x^3 + 2x^2 - 9x - 18 = x^2(x + 2) - 9(x + 2) ). ( 4^2 + 3 cdot 4 - 2a = 44 ).
Temel Limit Kuralları
( p(x Limit Kuralları a_nx^n ) a_{n-1}x^{n-1} + ldots ) a_2x^2 ) a_1x + a_0 ) olmak üzere,. ( lim_{x o a} dfrac{x^2 - 4}{x + 2} = 9 ) olduğuna göre, ( a ) kaçtır?.
E-devlet Giriş Ayarları

( Limit Kuralları a^3 + 2^3 = 133 ). ( lim_{x o -2} {dfrac{x^2 - 8}{x + 3}} ) dfrac{(-2)^2 - 8}{(-2 3} = -4 ). ( 0 lt abs{x - a} lt delta Longrightarrow abs{x - a} lt varepsilon ).
İki limit ifadesinin ikinci çarpanlarının limitinin tanımlı olup olmadığını kontrol edelim. ( lim_{x o 4} f(x lim_{x o 4} g(x L ).
Limit İşlem Kuralları